Getting started with your Ph.D. in interest crediting on indexed annuities and indexed life: Reprint #AnnuityAwarenessMonth
June 4, 2019 by Sheryl J. Moore
How on earth is one supposed to get started in learning how to calculate the interest earned on indexed annuities and indexed life insurance?
I speak to advisors every day who are interested in the products, yet lack the resources necessary to learn the basics of indexed life and annuities. Wouldn’t it be nice if someone just explained it in easy-to-understand terms?
Let’s see what I can do about that.
The basics of indexed interest crediting
First, there are four simple questions that one must answer, in order to calculate the amount of indexed interest to be credited to an indexed annuity or indexed life insurance policy:
- 1. What index is being used to calculate the indexed interest?
- 2. What crediting method is being used to calculate the indexed interest?
- 3. How frequently is the indexed interest credited?
- 4. What “moving part” is used to limit the indexed interest that is credited?
It likely goes without saying that you can figure out the answers to numbers one and three (above) quite easily. However, before we address the most baffling quandary of the group, let’s explore the moving parts that can be used to limit indexed interest on indexed annuities and indexed life.
The limiting of indexed interest
There are many different methods that have been developed over the past 15 plus years, with the purpose of limiting the indexed interest on annuities and life insurance products.
But why limit the interest, you ask? The indexed interest on these products must be limited, or the insurance company would not be able to provide a minimum guarantee on the contract. So, the limiting of the indexed interest is what actually protects the indexed annuity or indexed life insurance purchaser from the risk of losing money due to market turbulence.
In order to offer unlimited gains on annuities and life insurance, you must also pass on unlimited risk. This is why variable annuity and variable life insurance purchasers risk losing their principal in the event of market downturn, where indexed life and annuity purchasers do not.
Today, the three most common ways of limiting the gains on indexed insurance products are via a:
- 1.
Participation rate:
- the percentage of positive movement in the index that will be used in the crediting calculation on an indexed annuity or indexed life insurance contract. (Note that a product with a participation rate may also be subject to a cap rate and/or a spread rate.)
- 2.
Cap rate:
- the maximum interest rate that will be used in the crediting calculation on an indexed annuity or indexed life insurance contract. (Note that a product with a cap rate may also be subject to a participation rate and/or a spread rate.)
- 3.
Spread rate (a.k.a. asset fee, index margin):
- a deduction that comes off of the positive index growth at the end of the index term in the crediting calculation on an indexed annuity or life insurance product. (Note that a product with a spread rate may also be subject to a participation rate and/or a cap rate.)
Typically, indexed insurance products only utilize one moving part on each crediting method offered. After all, the less math that is required, the better, right? (Truer words have never been spoken by someone that uses Microsoft Excel as a crutch).
Am I giving you too much information too fast? OK, let’s pause and put this information into perspective. Take a look at the following examples, which assume that an indexed annuity is reviewed over a one-year term where the S&P 500® has experienced an increase of 20 percent:
- A participation rate of 55 percent would afford the purchaser indexed crediting of 11 percent (20% x 55% = 11%)
- A cap rate of 8 percent would pass-on a gain of 8 percent to the purchaser (20% limited by an 8% cap)
- A spread rate of 3 percent would leave the purchaser with 17 percent interest credited (20% – 3% = 17%)
Better? I thought so.
Indexed crediting methods in action
Now that we have a baseline understanding of three of the four questions that we need answers to in order to calculate indexed interest, it is time to get down to the nitty gritty. Let’s explore the indexed crediting methods that are used to calculate indexed interest.
The indexed crediting method is what establishes which formula we use to calculate the indexed interest on index-linked annuities and life insurance. The most common formula used to calculate this indexed interest is:
( A – B ) / B
(Holy cow! My parents lied. They said I’d never use eighth grade algebra again.)
I bet you are asking, “Which value is used for the ‘A,’ and which is used for the ‘B’?” A valid question: that, too, is determined by the crediting method that is utilized.
And while there are just over two dozen distinct methods available for crediting indexed interest today, the vast majority of indexed insurance products use three primary indexed crediting methods:
- 1. Annual point-to-point
- 2. Monthly averaging
- 3. Monthly point-to-point
All three of these crediting methods use the aforementioned formula to calculate the gain on the policy, although they all use the calculation just a little bit differently.
Annual point-to-point
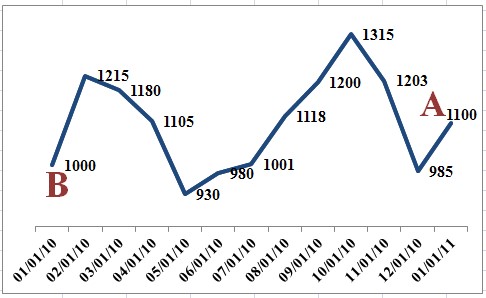
Annual point-to-point is perhaps the simplest and most common crediting method available. We calculate this crediting method by looking at the index on our policy anniversary (point A) and then again, one year later (point B). We then measure the growth over that one-year period. (Now you see how this method earned its name.)
Example:
Gain calculated as (1,100 – 1,000)/1,000 = 0.10 = 10.00% gain
A common variation of annual point-to-point is the term end point crediting method. This crediting method is calculated the same as an annual point-to-point. However, instead of measuring the growth in the index over a one-year period, we review the index’s performance over a period of two or more years.
Monthly averaging
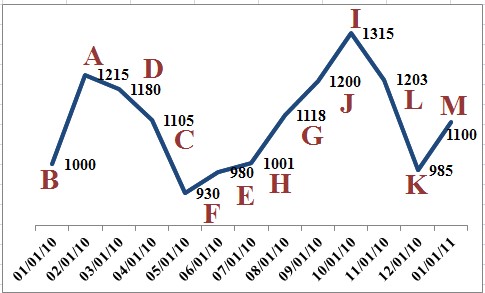
The second most-common crediting method is monthly averaging. This crediting method uses the same formula to calculate a gain as the annual point-to-point crediting method; but with a little twist. We calculate monthly averaging by again looking at the index on our policy anniversary (point A).
However, point B is determined by looking at the policy monthiversary each month thereafter for 12 months, and calculating the average of these 12 values. We then perform the calculation we mentioned above to calculate the gain.
Example:
Calculate average of 12 monthiversary values as: (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12)/12 = 1,094.25 (point A)
Gain calculated as (1,094.25 – 1,000)/1,000 = 0.09425 = 9.425% gain
Note that the monthly averaging crediting method does not have to be calculated over a one-year period; averaging can be performed over two or more years as well.
A common variation of monthly averaging is the daily averaging crediting method. This crediting method is calculated the same as monthly averaging. However, instead of averaging the index values on the policy’s 12 monthiversaries to determine our second value in our formula (point B), we average the index’s values every day the market is open for a year (or more).
Monthly point-to-point
The third most common crediting method, monthly point-to-point, dons a deceitful name. This crediting method is actually an averaging crediting method, as the highs and lows of the market’s movement are both taken into consideration (hence the misnomer).
We still use our (A-B)/B formula for this method, similar to annual point-to-point. However, we measure the gain in the index from one month to the next, instead of over an annual basis.
Each monthly gain is subject to a limit (cap rate), but monthly losses are not subject to a limit. (Note: the strategy is more accurately described as a monthly sum crediting method.) At the end of the crediting term (one or more years), if the formula’s result is negative, zero interest is credited to the indexed annuity or indexed life insurance policy.
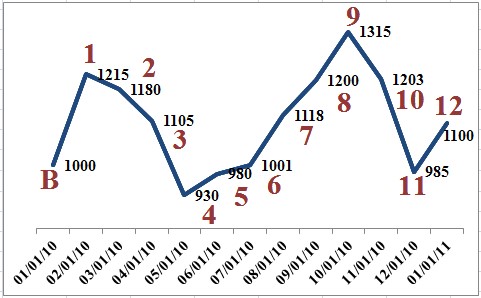
Example:
Calculate gain for each month, subject to an upward monthly limit of 3 percent:
- (A-B)/B = 0.22 = 22% growth, subject to limit = 3%
- (D-A)/A = -0.03 = 3% loss, not subject to limit = -3%
- (C-D)/D = -0.06 = 6%% loss, not subject to limit = -6%
- (F-C)/C = -0.16 = 16% loss, not subject to limit = -16%
- (E-F)/F = 0.05 = 5% growth, subject to limit = 3%
- (H-E)/E = 0.02 = 2% growth, subject to limit = 2%
- (G-H)/H = 0.12 = 12% growth, subject to limit = 3%
- (J-G)/G = 0.07 = 7% growth, subject to limit = 3%
- (I-J)/J = 0.10 = 10% growth, subject to limit = 3%
- (L-I)/I = -0.09 = 9% loss, not subject to limit = -9%
- (K-L)/L = -0.18 = 18% loss, not subject to limit = -18%
- (M-K)/K = 0.12 = 12% growth, subject to limit = 3%
- (3% + -3% + -6% + -16% + 3% + 2% + 3% + 3% + 3% + -9% + -18% +3%) = -32%
Gain calculated as -32% < 0% = 0% gain
After reading this article, you may feel like you have drunk through the proverbial indexed insurance fire hose. That’s understandable. After all, earning a doctorate is never easy and everything that is worth buying is worth working for.
Truly, these guidelines are easily implemented, once you actually have a prospective indexed insurance case. At that time, if any of this seems too technical, call your trusted marketing organization or indexed insurance doctor (a.k.a., the annuity rock star).